https://arxiv.org/abs/1901.10155
Introduction
PUの問題設定として、Single Training SetとCase Controlがある。その上、識別器を訓練する方法が主流で、生成モデルでとらえようとするのは少ない。識別器訓練の手法は早期はSample Selectionが主流だったが、📄2014-NIPS-[Ramp]Analysis of Learning from Positive and Unlabeled Data 以降はSample Reweighting(Uを言い換えて重み付きのPとNの分類に変換する)
この研究では、長らく悲愁流だったSample Selectionの見地から手法開発を行い、SOTAレベルの性能を得た。以下の3点が貢献である。
- 表現力の高いモデルにおいて、どのようなPデータが学習するうえで効果が高いか。
- Noisy Labelでも使われている、DNNのMemorization Effectを使えば、Uの中のPデータは損失が高いということを識別できる。上手く損失関数を選べば、Pデータをくくりだせたりする。
- Positiveの選択バイアスがある場合、どのようにできるだけ影響されずに学習するか?を考えた。(提案手法のSample Selectionで)
提案手法はadaptively augmented PU (aaPU)として、訓練のたびにUからPを選び出して、それを次のループ以降本物のPとして扱いながら訓練する感じ。
既存の昔のSample Selectionの手法は表現能力の高いモデルに対して強くないが、aaPUでは表現能力の高いモデルに対しても問題はない。この手法は、自己教師あり学習のラベル付けをサボって楽にさせることもできる。
問題設定
- 入力はであり、ラベルは二値分類でである。
- PUでは、データ分布は以下のようになる。
- Unlabeled
- Positive
- Positive
- Class Priorが定義されている。
- 損失関数は正の値を取ると0に、負の値を取ると0以上の損失を与える。
- PUやPNのrisk最小化の式で現れる各部分の略記号。
提案手法
DNNではMemorization Effetctがある(📄2020-Survey-A Survey of Label-noise Representation Learning: Past, Present and Future 参照)。これから着想を受けると、Unlabeledの中で、Lossが大きいのはNegativeにするべきではなく、Positiveである可能性が高いので、以後の訓練でPositiveとして扱うというものである。
実際に、Small Loss TrickはPUでも同様に働き、訓練が進むにつれてnnPU 📄2017-NIPS-[nnPU] Positive-Unlabeled Learning with Non-Negative Risk Estimator においてのUnlabeledの中の各サンプルの損失は以下のようになった。
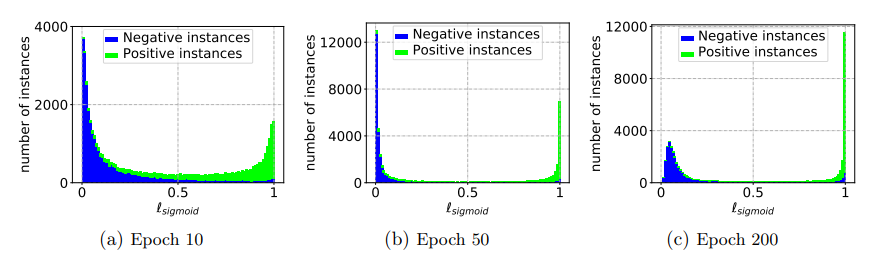
この研究では、うまいことPを選び出すための方法を考えていく。その前に、nnPUはOverfittingを防ぐためGradient Ascentを適宜行っていて、Small Loss Trickで損失の大小を参考にサンプルを選ぶとき。単純に損失の大小関係で評価する以上uPU 📄2015-ICML-[uPU] Convex Formulation for Learning from Positive and Unlabeled Data でもよさそうであるが、過学習しすぎて大きな損失の部分はPositive in Uであるけどそれ以上に大量のPositive in Uも損失が0になってる(過学習)ので不適切。下図のように。
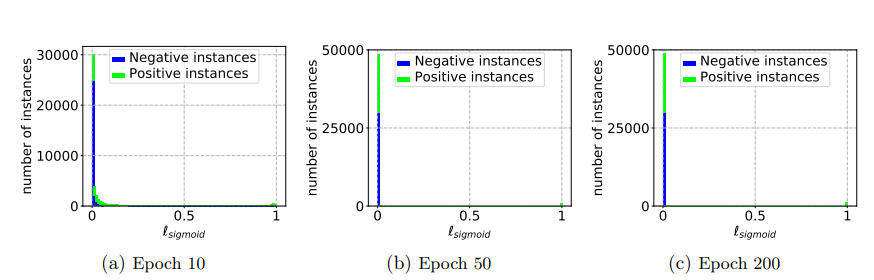
損失関数に関しても、Sigmoid Lossを使うよりは以下のLog Lossのほうがいい(当たり前だろ…)
どのようにUの中からPを選び出すか
Uの中から特定したデータをPにそのまま追加するのはうまく行かないらしい。(下の図のように混ざってしまうので)
Negativeとみなして計算しているUnlabeledの中の、本来Positiveの分布に従うものの損失の期待値と考えれば、この式で損失を計算した時に大きい値を取るのがPositiveである。
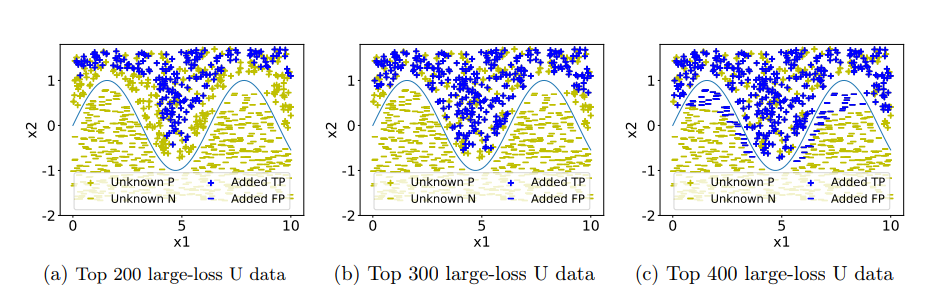
これで計算してみると、top-x %を採れば解決というわけではないのがよくわかる。そして、確実に安全にPositiveなものをとろうとするなら、biasが生じることになる。
そして、この手法は基本的にはnnPUで計算するが、Positive in Uで一旦見つけたものはUから排除する。なぜなら、nnPUのようにとしていても、過学習傾向にあってしまうから。それならば、Positive in Uとして、Positive扱いでも、この部分の計算からは排除すればよい。
思索: これ、Domain Shiftをかんがえてちゃんとclass priorやバイアス排除の手法を適用させた方が良いのでは。
つまり、以下の式の最小化である。が選んだものの集合で、はすべて排他的。
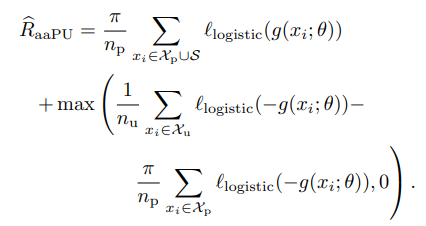
アルゴリズム

ここでclass prior変わってないけどええんか?
small loss trick系列なので、途中までnnPUを使い、一定の訓練水準に達したらこの手法を使って、からを選びだす。
Result
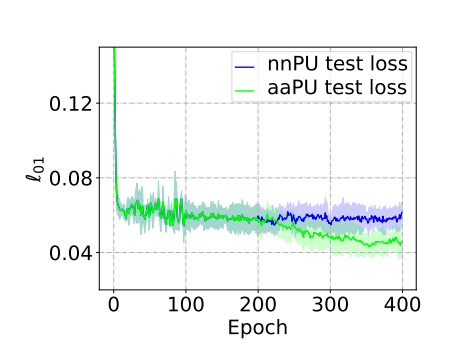
sinを、三層のDNNによって予測している。nnPUに比べて、一定epoch後も損失が減り続けているとわかる。
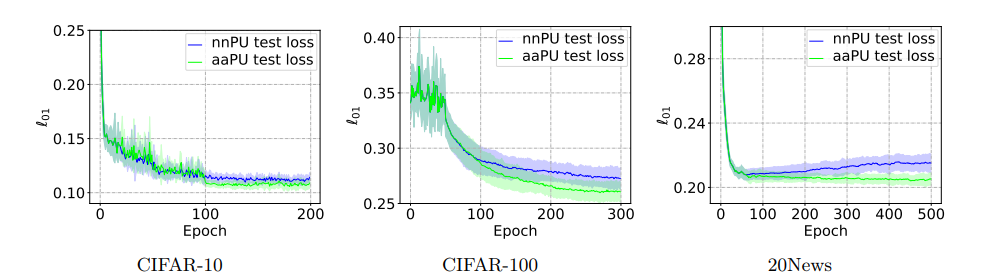
Real Dataについても、依然と有効だとわかる。とくに20 NewsはnnPUでさえ過学習が起きている。
